Как представляются в компьютере целые числа?
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака
Обычно занимают в памяти компьютера один или два байта. В однобайтовом формате принимают значения от 000000002 до 111111112. В двубайтовом формате - от 00000000 000000002 до 11111111 111111112.
Диапазоны значений целых чисел без знака
| Формат числа в байтах | Диапазон | ||||
| Запись с порядком | Обычная запись | ||||
| 1 | 0 ... 28-1 | 0 ... 255 | |||
| 2 | 0 ... 216-1 | 0 ... 65535 |
Примеры:
а) число 7210 = 10010002 в однобайтовом формате:
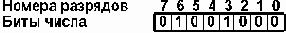
б) это же число в двубайтовом
формате:

в) число 65535 в двубайтовом
формате:
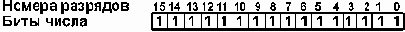
Целые числа со знаком
Обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа.
Диапазоны значений целых чисел со знаком
| Формат числа в байтах | Диапазон | ||||
| Запись с порядком | Обычная запись | ||||
| 1 | -27 ... 27-1 | -128 ... 127 | |||
| 2 | -215 ... 215-1 | -32768 ... 32767 | |||
| 4 | -231 ... 231-1 | -2147483648 ... 2147483647 |
Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины - семь разрядов.
| В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код. |
Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией cложения.
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково - двоичными кодами с цифрой 0 в знаковом разряде. Например:

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Например:
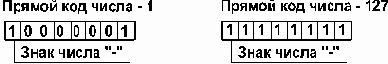
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями. Например:

3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Например:
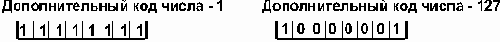
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
