Данные
Носители данных
Данные — диалектическая составная часть информации. Они представляют собой зарегистрированные сигналы. При этом физический метод регистрации может быть любым: механическое перемещение физических тел, изменение их формы или параметров качества поверхности, изменение электрических, магнитных, оптических характеристик, химического состава и (или) характера химических связей, изменение состояния электронной системы и многое другое. В соответствии с методом регистрации данные могут храниться и транспортироваться на носителях различных видов.
Самым распространенным носителем данных, хотя и не самым экономичным, по-видимому, является бумага. На бумаге данные регистрируются путем изменения оптических характеристик ее поверхности. Изменение оптических свойств (изменение коэффициента отражения поверхности в определенном диапазоне длин волн) используется также в устройствах, осуществляющих запись лазерным лучом на пластмассовых носителях с отражающим покрытием (CD-ROM). В качестве носителей, использующих изменение магнитных свойств, можно назвать магнитные ленты и диски. Регистрация данных путем изменения химического состава поверхностных веществ носителя широко используется в фотографии. На биохимическом уровне происходит накопление и передача данных в живой природе.
Носители данных интересуют нас не сами по себе, а постольку, поскольку свойства информации весьма тесно связаны со свойствами ее носителей. Любой носитель можно характеризовать параметром разрешающей способности (количеством данных, записанных в принятой для носителя единице измерения) и динамическим диапазоном (логарифмическим отношением интенсивности амплитуд максимального и минимального регистрируемого сигналов). От этих свойств носителя нередко зависят такие свойства информации, как полнота, доступность и достоверность. Так, например, мы можем рассчитывать на то, что в базе данных, размещаемой на компакт-диске, проще обеспечить полноту информации, чем в аналогичной по назначению базе данных, размещенной на гибком магнитном диске, поскольку в первом случае плотность записи данных на единице длины дорожки намного выше.
Для обычного потребителя доступность информации в книге заметно выше, чем той же информации на компакт-диске, поскольку не все потребители обладают необходимым оборудованием. И, наконец, известно, что визуальный эффект от просмотра слайда в проекторе намного больше, чем от просмотра аналогичной иллюстрации, напечатанной на бумаге, поскольку диапазон яркостных сигналов в проходящем свете на два-три порядка больше, чем в отраженном.
Задача преобразования данных с целью смены носителя относится к одной из важнейших задач информатики. В структуре стоимости вычислительных систем устройства для ввода и вывода данных, работающие с носителями информации, составляют до половины стоимости аппаратных средств.
Операции с данными
В ходе информационного процесса данные преобразуются из одного вида в другой с помощью методов. Обработка данных включает в себя множество различных операций. По мере развития научно-технического прогресса и общего усложнения связей в человеческом обществе трудозатраты на обработку данных неуклонно возрастают. Прежде всего, это связано с постоянным усложнением условий управления производством и обществом. Второй фактор, также вызывающий общее увеличение объемов обрабатываемых данных, тоже связан с научно-техническим прогрессом, а именно с быстрыми темпами появления и внедрения новых носителей данных, средств их хранения и доставки.
В структуре возможных операций с данными можно выделить следующие основные:
• сбор данных—накопление информации с целью обеспечения достаточной полноты для принятия решений;
• формализация данных — приведение данных, поступающих из разных источников, к одинаковой форме, чтобы сделать их сопоставимыми между собой, то есть повысить их уровень доступности;
• фильтрация данных — отсеивание «лишних» данных, в которых нет необходимости для принятия решений; при этом должен уменьшаться уровень «шума», а достоверность и адекватность данных должны возрастать;
• сортировка данных — упорядочение данных по заданному признаку с целью удобства использования; повышает доступность информации;
- архивация данных — организация хранения данных в удобной и легкодоступной форме; служит для снижения экономических затрат по хранению данных и повышает общую надежность информационного процесса в целом;
• защита данных — комплекс мер, направленных на предотвращение утраты, воспроизведения и модификации данных;
• транспортировка данных—прием и передача (доставка и поставка) данных междуудаленными участниками информационного процесса; при этом источник данных в информатике принято называть сервером, а потребителя — клиентом;
• преобразование данных — перевод данных из одной формы в другую или изодной структуры в другую. Преобразование данных часто связано с изменением типа носителя, например книги можно хранить в обычной бумажной форме,но можно использовать для этого и электронную форму, и микрофотопленку. Необходимость в многократном преобразовании данных возникает также приих транспортировке, особенно если она осуществляется средствами, не предназначенными для транспортировки данного вида данных. В качестве примераможно упомянуть, что для транспортировки цифровых потоков данных по каналамтелефонных сетей (которые изначально были ориентированы только на передачу аналоговых сигналов в узком диапазоне частот) необходимо преобразование цифровых данных в некое подобие звуковых сигналов, чем и занимаются специальные устройства — телефонные модемы.
Приведенный здесь список типовых операций с данными далеко не полон. Миллионы людей во всем мире занимаются созданием, обработкой, преобразованием и транспортировкой данных, и на каждом рабочем месте выполняются свои специфические операции, необходимые для управления социальными, экономическими, промышленными, научными и культурными процессами. Полный список возможных операций составить невозможно, да и не нужно. Сейчас нам важен другой вывод: работа с информацией может иметь огромную трудоемкость, и ее надо автоматизировать.
Кодирование данных двоичным кодом
Для автоматизации работы с данными, относящимися к различным типам, очень важно унифицировать их форму представления — для этого обычно используется прием кодирования, то есть выражение данных одного типа через данные другого типа. Естественные человеческие языки — это не что иное, как системы кодирования понятий для выражения мыслей посредством речи. К языкам близко примыкают азбуки (системы кодирования компонентов языка с помощью графических символов). История знает интересные, хотя и безуспешные попытки создания «универсальных» языков и азбук. По-видимому, безуспешность попыток их внедрения связана с тем, что национальные и социальные образования естественным образом понимают, что изменение системы кодирования общественных данных непременно приводит к изменению общественных методов (то есть норм права и морали), а это может быть связано с социальными потрясениями.
Та же проблема универсального средства кодирования достаточно успешно реализуется в отдельных отраслях техники, науки и культуры. В качестве примеров можно привести систему записи математических выражений, телеграфную азбуку, морскую флажковую азбуку, систему Брайля для слепых и многое другое.
Своя система существует и в вычислительной технике — она называется двоичным кодированием и основана на представлении данных последовательностью всего двух знаков: 0 и 1. Эти знаки называются двоичными цифрами, по-английски — binary digit или сокращенно bit (бит).
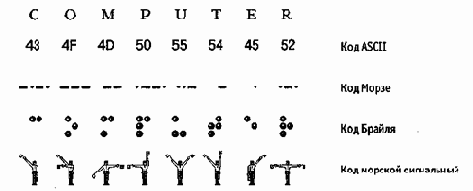
Рис. 1.2. Примеры различных систем кодирования
Одним битом могут быть выражены два понятия: 0 или 1 (да или нет, черное или белое, истина или ложь и т. п.). Если количество битов увеличить до двух, то уже можно выразить четыре различных понятия:
00 01 10 11
Тремя битами можно закодировать восемь различных значений:
000 001 010 011 100 101 ПО 111
Увеличивая на единицу количество разрядов в системе двоичного кодирования, мы увеличиваем в два раза количество значений, которое может быть выражено в данной системе, то есть общая формула имеет вид:
N=2m,
где N— количество независимых кодируемых значений;
т — разрядность двоичного кодирования, принятая в данной системе.
Кодирование целых и действительных чисел
Целые числа кодируются двоичным кодом достаточно просто — достаточно взять целое число и делить его пополам до тех пор, пока частное не будет равно единице. Совокупность остатков от каждого деления, записанная справа налево вместе с последним частным, и образует двоичный аналог десятичного числа.
19:2 = 9+1
9:2 = 4 + 1
4:2=2+0
2:2=1+0
Таким образом, 1910 = 100112.
Для кодирования целых чисел от 0 до 255 достаточно иметь 8 разрядов двоичного кода (8 бит). Шестнадцать бит позволяют закодировать целые числа от 0 до 65 535, а 24 бита — уже более 16,5 миллионов разных значений.
Для кодирования действительных чисел используют 80-разрядное кодирование. При этом число предварительно преобразуется в нормализованную форму:
3,1415926 = 0,31415926×101
300 000 = 0,3×106
123 456 789 = 0,123456789×1010
Первая часть числа называется мантиссой, а вторая — характеристикой. Большую часть из 80 бит отводят для хранения мантиссы (вместе со знаком) и некоторое фиксированное количество разрядов отводят для хранения характеристики (тоже со знаком).
Кодирование текстовых данных
Если каждому символу алфавита сопоставить определенное целое число (например, порядковый номер), то с помощью двоичного кода можно кодировать и текстовую информацию. Восьми двоичных разрядов достаточно для кодирования 256 различных символов. Этого хватит, чтобы выразить различными комбинациями восьми битов все символы английского и русского языков, как строчные, так и прописные, а также знаки препинания, символы основных арифметических действий и некоторые общепринятые специальные символы, например символ «§».
Технически это выглядит очень просто, однако всегда существовали достаточно веские организационные сложности. В первые годы развития вычислительной техники они были связаны с отсутствием необходимых стандартов, а в настоящее время вызваны, наоборот, изобилием одновременно действующих и противоречивых стандартов.
Для того чтобы весь мир одинаково кодировал текстовые данные, нужны единые таблицы кодирования, а это пока невозможно из-за противоречий между символами национальных алфавитов, а также противоречий корпоративного характера.
Для английского языка, захватившего де-факто нишу международного средства общения, противоречия уже сняты. Институт стандартизации США (ANSI—American National Standard Institute) ввел в действие систему кодирования ASCII (American Standard Code for Information Interchange — стандартный код информационного обмена США). В системе ASCII закреплены две таблицы кодирования — базовая и расширенная. Базовая таблица закрепляет значения кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.
Первые 32 кода базовой таблицы, начиная с нулевого, отданы производителям аппаратных средств (в первую очередь производителям компьютеров и печатающих устройств). В этой области размещаются так называемые управляющие коды, которым не соответствуют никакие символы языков, и, соответственно, эти коды не выводятся ни на экран, ни на устройства печати, но ими можно управлять тем, как производится вывод прочих данных.
Начиная с кода 32 по код 127 размещены коды символов английского алфавита, знаков препинания, цифр, арифметических действий и некоторых вспомогательных символов. Базовая таблица кодировки ASCII приведена в таблице 1.1.
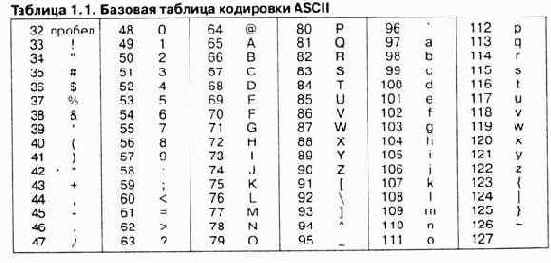
Аналогичные системы кодирования текстовых данных были разработаны и в других странах. Так, например, в СССР в этой области действовала система кодирования КОИ-7 (код обмена информацией, семизначный). Однако поддержка производителей оборудования и программ вывела американский код ASCII на уровень международного стандарта, и национальным системам кодирования пришлось «отступить» во вторую, расширенную часть системы кодирования, определяющую значения кодов со 128 по 255. Отсутствие единого стандарта в этой области привело к множественности одновременно действующих кодировок. Только в России можно указать три действующих стандарта кодировки и еще два устаревших.
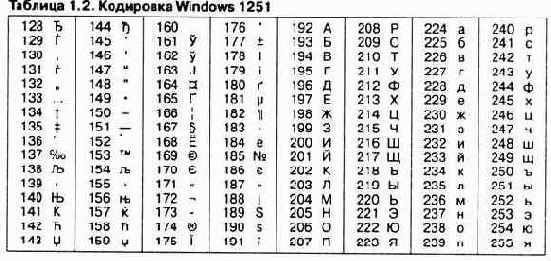
Так, например, кодировка символов русского языка, известная как кодировка Windows-1251, была введена «извне» — компанией Microsoft, но, учитывая широкое распространение операционных систем и других продуктов этой компании в России, она глубоко закрепилась и нашла широкое распространение (таблица 1.2). Эта кодировка используется на большинстве локальных компьютеров, работающих на платформе Windows.
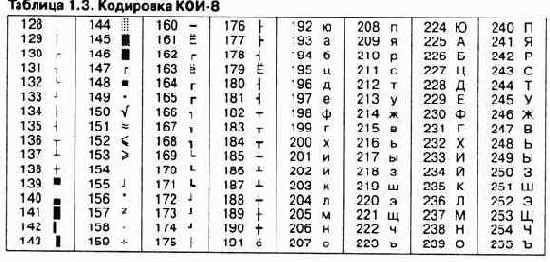
Другая распространенная кодировка носит название КОИ-8 (код обмена информацией, восьмизначный) — ее происхождение относится ко временам действия Совета Экономической Взаимопомощи государств Восточной Европы (таблица 1.3). Сегодня кодировка КОИ-8 имеет широкое распространение в компьютерных сетях на территории России и в российском секторе Интернета.
Международный стандарт, в котором предусмотрена кодировка символов русского алфавита, носит название кодировки /50 (International Standard Organization — Международный институт стандартизации). На практике данная кодировка используется редко (таблица 1.4).
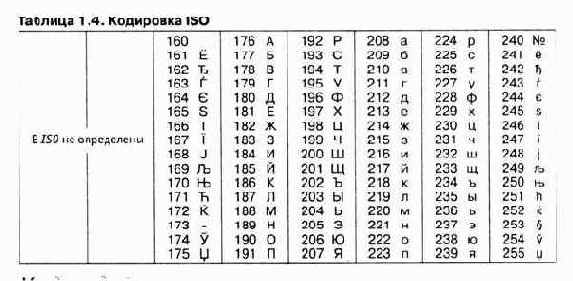
На компьютерах, работающих в операционных системах MS-DOS, могут действовать еще две кодировки (кодировка ГОСТ и кодировка ГОСТ-альтернативная). Первая из них считалась устаревшей даже в первые годы появления персональной вычислительной техники, но вторая используется и по сей день (см. таблицу 1.5).
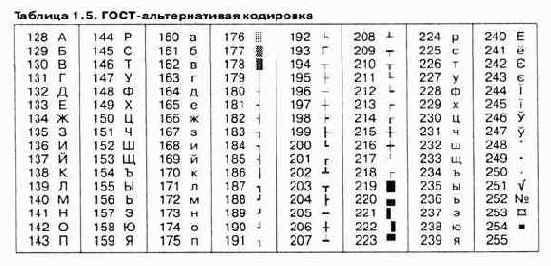
В связи с изобилием систем кодирования текстовых данных, действующих в России, возникает задача межсистемного преобразования данных — это одна из распространенных задач информатики.
Универсальная система кодирования текстовых данных
Если проанализировать организационные трудности, связанные с созданием единой системы кодирования текстовых данных, то можно прийти к выводу, что они вызваны ограниченным набором кодов (256). В то же время очевидно, что если, например, кодировать символы не восьмиразрядными двоичными числами, а числами с большим количеством разрядов, то и диапазон возможных значений кодов станет намного больше.
Такая система, основанная на 16- разрядном кодировании символов, получила название универсальной — UNICODE. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65 536 различных символов — этого поля достаточно для размещения в одной таблице символов большинства языков планеты.
Несмотря на тривиальную очевидность такого подхода, простой механический переход на данную систему долгое время сдерживался из-за недостаточных ресурсов средств вычислительной техники (в системе кодирования UNICODE все текстовые документы автоматически становятся вдвое длиннее). Во второй половине 90-х годов технические средства достигли необходимого уровня обеспеченности ресурсами, и сегодня мы наблюдаем постепенный перевод документов и программных средств на универсальную систему кодирования. Для индивидуальных пользователей это еще больше добавило забот по согласованию документов, выполненных в разных системах кодирования, с программными средствами, но это надо понимать как трудности переходного периода.
Кодирование графических данных
 |
издавна принятый в полиграфии
Если рассмотреть с помощью увеличительного стекла черно-белое графическое изображение, напечатанное в газете или книге, то можно увидеть, что оно состоит из мельчайших точек, образующих характерный узор, называемый растром (рис. 1.3).
Поскольку линейные координаты и индивидуальные свойства каждой точки (яркость) можно выразить с помощью целых чисел, то можно сказать, что растровое кодирование позволяет использовать двоичный код для представления графических данных. Общепринятым на сегодняшний день считается представление черно-белых иллюстраций в виде комбинации точек с 256 градациями серого цвета, и, таким образом, для кодирования яркости любой точки обычно достаточно восьмиразрядного двоичного числа.
Для кодирования цветных графических изображений применяется принцип декомпозиции произвольного цвета на основные составляющие.
В качестве таких составляющих используют три основные цвета: красный (Red, К), зеленый (Green, G) и синий (Blue, В). На практике считается (хотя теоретически это не совсем так), что любой цвет, видимый человеческим глазом, можно получить путем механического смешения этих трех основных цветов. Такая система кодирования называется системой RGB по первым буквам названий основных цветов.
Если для кодирования яркости каждой из основных составляющих использовать по 256 значений (восемь двоичных разрядов), как это принято для полутоновых черно-белых изображений, то на кодирование цвета одной точки надо затратить 24 разряда. При этом система кодирования обеспечивает однозначное определение 16,5 млн различных цветов, что на самом деле близко к чувствительности человеческого глаза. Режим представления цветной графики с использованием 24 двоичных разрядов называется полноцветным (True Color).
Каждому из основных цветов можно поставить в соответствие дополнительный цвет, то есть цвет, дополняющий основной цвет до белого. Нетрудно заметить, что для любого из основных цветов дополнительным будет цвет, образованный суммой пары остальных основных цветов. Соответственно, дополнительными цветами являются: голубой (Cyan, С), пурпурный (Magenta, M) и желтый (Yellow, У). Принцип декомпозиции произвольного цвета на составляющие компоненты можно применять не только для основных цветов, но и для дополнительных, то есть любой цвет можно представить в виде суммы голубой, пурпурной и желтой составляющей. Такой метод кодирования цвета принят в полиграфии, но в полиграфии используется еще и четвертая краска — черная (Black, К). Поэтому данная система кодирования обозначается четырьмя буквами CMYK (черный цвет обозначается буквой К, потому, что буква В уже занята синим цветом), и для представления цветной графики в этой системе надо иметь 32 двоичных разряда. Такой режим тоже называется полноцветным (True Color).
Если уменьшить количество двоичных разрядов, используемых для кодирования цвета каждой точки, то можно сократить объем данных, но при этом диапазон кодируемых цветов заметно сокращается.
Кодирование цветной графики 16- разрядными двоичными числами называется режимом High Color.
При кодировании информации о цвете с помощью восьми бит данных можно передать только 256 цветовых оттенков. Такой метод кодирования цвета называется индексным. Смысл названия в том, что, поскольку 256 значений совершенно недостаточно, чтобы передать весь диапазон цветов, доступный человеческому глазу, код каждой точки растра выражает не цвет сам по себе, а только его номер (индекс) в некоей справочной таблице, называемой палитрой. Разумеется, эта палитра должна прикладываться к графическим данным — без нее нельзя воспользоваться методами воспроизведения информации на экране или бумаге (то есть, воспользоваться, конечно, можно, но из-за неполноты данных полученная информация не будет адекватной: листва на деревьях может оказаться красной, а небо — зеленым).
Кодирование звуковой информации
Приемы и методы работы со звуковой информацией пришли в вычислительную технику наиболее поздно. К тому же, в отличие от числовых, текстовых и графических данных, у звукозаписей не было столь же длительной и проверенной истории кодирования. В итоге методы кодирования звуковой информации двоичным кодом далеки от стандартизации. Множество отдельных компаний разработали свои корпоративные стандарты, но если говорить обобщенно, то можно выделить два основных направления.
Метод FM (Frequency Modulation) основан на том, что теоретически любой сложный звук можно разложить на последовательность простейших гармонических сигналов разных частот, каждый из которых представляет собой правильную синусоиду, а следовательно, может быть описан числовыми параметрами, то есть кодом. В природе звуковые сигналы имеют непрерывный спектр, то есть являются аналоговыми. Их разложение в гармонические ряды и представление в виде дискретных цифровых сигналов выполняют специальные устройства — аналогово-цифровые преобразователи (АЦП). Обратное преобразование для воспроизведения звука, закодированного числовым кодом, выполняют цифро-аналоговые преобразователи (ДАЛ).
При таких преобразованиях неизбежны потери информации, связанные с методом кодирования, поэтому качество звукозаписи обычно получается не вполне удовлетворительным и соответствует качеству звучания простейших электромузыкальных инструментов с окрасом, характерным для электронной музыки. В то же время данный метод кодирования обеспечивает весьма компактный код, и потому он нашел применение еще в те годы, когда ресурсы средств вычислительной техники были явно недостаточны.
Метод таблично-волнового ( Wave-Table) синтеза лучше соответствует современному уровню развития техники. Если говорить упрощенно, то можно сказать, что где-то в заранее подготовленных таблицах хранятся образцы звуков для множества различных музыкальных инструментов (хотя не только для них). В технике такие образцы называют сэмплами. Числовые коды выражают тип инструмента, номер его модели, высоту тона, продолжительность и интенсивность звука, динамику его изменения, некоторые параметры среды, в которой происходит звучание, а также прочие параметры, характеризующие особенности звука. Поскольку в качестве образцов используются «реальные» звуки, то качество звука, полученного в результате синтеза, получается очень высоким и приближается к качеству звучания реальных музыкальных инструментов.
Основные структуры данных
Работа с большими наборами данных автоматизируется проще, когда данные упорядочены, то есть образуют заданную структуру. Существует три основных типа структур данных: линейная, иерархическая и табличная. Их можно рассмотреть на примере обычной книги.
Если разобрать книгу на отдельные листы и перемешать их, книга потеряет свое назначение. Она по-прежнему будет представлять набор данных, но подобрать адекватный метод для получения из нее информации весьма непросто. (Еще хуже дело будет обстоять, если из книги вырезать каждую букву отдельно — в этом случае вряд ли вообще найдется адекватный метод для ее прочтения.)
Если же собрать все листы книги в правильной последовательности, мы получим простейшую структуру данных — линейную. Такую книгу уже можно читать, хотя для поиска нужных данных ее придется прочитать подряд, начиная с самого начала, что не всегда удобно.
Для быстрого поиска данных существует иерархическая структура. Так, например, книги разбивают на части, разделы, главы, параграфы и т. п. Элементы структуры более низкого уровня входят в элементы структуры более высокого уровня: разделы состоят из глав, главы из параграфов и т. д.
Для больших массивов поиск данных в иерархической структуре намного проще, чем в линейной, однако и здесь необходима навигация, связанная с необходимостью просмотра. На практике задачу упрощают тем, что в большинстве книг есть вспомогательная перекрестная таблица, связывающая элементы иерархической структуры с элементами линейной структуры, то есть связывающая разделы, главы и параграфы с номерами страниц. В книгах с простой иерархической структурой, рассчитанных на последовательное чтение, эту таблицу принято называть оглавлением, а в книгах со сложной структурой, допускающей выборочное чтение, ее называют содержанием.
Линейные структуры (списки данных, векторы данных)
Линейные структуры — это хорошо знакомые нам списки. Список — это простейшая структура данных, отличающаяся тем, что каждый элемент данных однозначно определяется своим номером в массиве. Проставляя номера на отдельных страницах рассыпанной книги, мы создаем структуру списка. Обычный журнал посещаемости занятий, например, имеет структуру списка, поскольку все студенты группы зарегистрированы в нем под своими уникальными номерами. Мы называем номера уникальными потому, что в одной группе не могут быть зарегистрированы два студента с одним и тем же номером.
При создании любой структуры данных надо решить два вопроса: как разделять элементы данных между собой и как разыскивать нужные элементы. В журнале посещаемости, например, это решается так: каждый новый элемент списка заносится с новой строки, то есть разделителем является конец строки. Тогда нужный элемент можно разыскать по номеру строки.
N п/п Фамилия, Имя, Отчество
1 Аистов Александр Алексеевич
2 Бобров Борис Борисович
3 Воробьева Валентина Владиславовна
………………………………………………..
27 Сорокин Сергей Семенович
Разделителем может быть и какой- нибудь специальный символ. Нам хорошо известны разделители между словами — это пробелы. В русском и во многих европейских языках общепринятым разделителем предложений является точка. В рассмотренном нами классном журнале в качестве разделителя можно использовать любой символ, который не встречается в самих данных, например символ «*». Тогда наш список выглядел бы так:
Аистов Александр Алексеевич * Бобров Борис Борисович * Воробьева Валентина Владиславовна *... * Сорокин Сергей Семенович
В этом случае для розыска элемента с номером п надо просмотреть список начиная с самого начала и пересчитать встретившиеся разделители. Когда будет отсчитано n-i разделителей, начнется нужный элемент. Он закончится, когда будет встречен следующий разделитель.
Еще проще можно действовать, если все элементы списка имеют равную длину. В этом случае разделители в списке вообще не нужны. Для розыска элемента с номером п надо просмотреть список с самого начала и отсчитать а(и-1) символ, где а — длина одного элемента. Со следующего символа начнется нужный элемент. Его длина тоже равна а, поэтому его конец определить нетрудно. Такие упрощенные списки, состоящие из элементов равной длины, называют векторами данных. Работать с ними особенно удобно.
Таким образом, линейные структуры данных (списки) — это упорядоченные структуры, в которых адрес элемента однозначно определяется его номером.
Табличные структуры (таблицы данных, матрицы данных)
С таблицами данных мы тоже хорошо знакомы, достаточно вспомнить всем известную таблицу умножения. Табличные структуры отличаются от списочных тем, что элементы данных определяются адресом ячейки, который состоит не из одного параметра, как в списках, а из нескольких.
Для таблицы умножения, например, адрес ячейки определяется номерами строки и столбца. Нужная ячейка находится на их пересечении, а элемент выбирается из ячейки.
При хранении табличных данных количество разделителей должно быть больше, чем для данных, имеющих структуру списка. Например, когда таблицы печатают в книгах, строки и столбцы разделяют графическими элементами — линиями вертикальной и горизонтальной разметки (рис. 1.4).
Если нужно сохранить таблицу в виде длинной символьной строки, используют один символ-разделитель между элементами, принадлежащими одной строке, и другой разделитель для отделения строк, например так:
Меркурий*0,39*0,056*0#Ввнера*0,67*0,88*0#Земля*1,0*1(0*1#Марс*1)б1*0,1*2#...
|
Планета |
Расстояние до Солнца, а.е. |
Относительная масса |
Количество спутников |
|
Меркурий |
0,39 |
0,056 |
0 |
|
Венера |
0,67 |
0,88 |
0 |
|
Земля |
1,0 |
1,0 |
1 |
|
Марс |
1,51 |
0,1 |
2 |
|
Юпитер |
5,2 |
318 |
16 |
два типа разделителей — вертикальные и горизонтальные
Для розыска элемента, имеющего адрес ячейки (т,п), надо просмотреть набор данных с самого начала и пересчитать внешние разделители. Когда будет отсчитан т-1 разделитель, надо пересчитывать внутренние разделители. После того как будет найден и-1 разделитель, начнется нужный элемент. Он закончится, когда будет встречен любой очередной разделитель.
Еще проще можно действовать, если все элементы таблицы имеют равную длину. Такие таблицы называют матрицами. В данном случае разделители не нужны, поскольку все элементы имеют равную длину и количество их известно. Для розыска элемента с адресом (т, п) в матрице, имеющей М строк и N столбцов, надо просмотреть ее с самого начала и отсчитать a [N(m -1) + (п -1)] символ, где а — длина одного элемента. Со следующего символа начнется нужный элемент. Его длина тоже равна а, поэтому его конец определить нетрудно.
Таким образом, табличные структуры данных (матрицы) — это упорядоченные структуры, в которых адрес элемента определяется номером строки и номером столбца, на пересечении которых находится ячейка, содержащая искомый элемент.
Многомерные таблицы. Выше мы рассмотрели пример таблицы, имеющей два измерения (строка и столбец), но в жизни нередко приходится иметь дело с таблицами, у которых количество измерений больше. Вот пример таблицы, с помощью которой может быть организован учет учащихся.
Номер факультета: 3
Номер курса (на факультете): 2
Номер специальности (на курсе): 2
Номер группы в потоке одной специальности: 1
Номер учащегося в группе: 19
Размерность такой таблицы равна пяти, и для однозначного отыскания данных об учащемся в подобной структуре надо знать все пять параметров (координат).
Иерархические структуры данных
Нерегулярные данные, которые трудно представить в виде списка или таблицы, часто представляют в виде иерархических структур. С подобными структурами мы очень хорошо знакомы по обыденной жизни. Иерархическую структуру имеет система почтовых адресов. Подобные структуры также широко применяют в научных систематизациях и всевозможных классификациях (рис. 1.5).
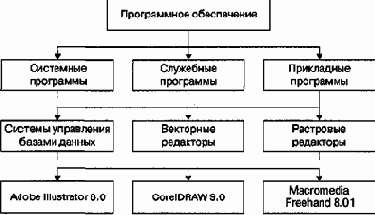
Рис. 1.5. Пример иерархической структуры данных
В иерархической структуре адрес каждого элемента определяется путем доступа (маршрутом), ведущим от вершины структуры к данному элементу. Вот, например, как выглядит путь доступа к команде, запускающей программу Калькулятор (стандартная программа компьютеров, работающих в операционной системе Windows 98):
Пуск > Программы > Стандартные > Калькулятор.
Дихотомия данных. Основным недостатком иерархических структур данных является увеличенный размер пути доступа. Очень часто бывает так, что длина маршрута оказывается больше, чем длина самих данных, к которым он ведет.
Поэтому в информатике применяют методы для регуляризации иерархических структур с тем, чтобы сделать путь доступа компактным. Один из методов получил название дихотомии. Его суть понятна из примера, представленного на рис. 1.6.
В иерархической структуре, построенной методом дихотомии, путь доступа к любому элементу можно представить как путь через рациональный лабиринт с поворотами налево (0) или направо (1) и, таким образом, выразить путь доступа в виде компактной двоичной записи. В нашем примере путь доступа к текстовому процессору Word 2000 выразится следующим двоичным числом: 1010.
Упорядочение структур данных
Списочные и табличные структуры являются простыми. Ими легко пользоваться, поскольку адрес каждого элемента задается числом (для списка), двумя числами (для двумерной таблицы) или несколькими числами для многомерной таблицы. Они также легко упорядочиваются. Основным методом упорядочения является сортировка. Данные можно сортировать по любому избранному критерию, например: по алфавиту, по возрастанию порядкового номера или по возрастанию какого-либо параметра.
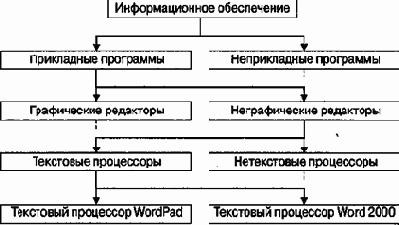
Рис. 1.6. Пример, поясняющий принцип действия метода дихотомии
Несмотря на многочисленные удобства, у простых структур данных есть и недостаток — их трудно обновлять. Если, например, перевести студента из одной группы в другую, изменения надо вносить сразу в два журнала посещаемости; при этом в обоих журналах будет нарушена списочная структура. Если переведенного студента вписать в конец списка группы, нарушится упорядочение по алфавиту, а если его вписать в соответствии с алфавитом, то изменятся порядковые номера всех студентов, которые следуют за ним.
Таким образом, при добавлении произвольного элемента в упорядоченную структуру списка может происходить изменение адресных данных у других элементов. В журналах успеваемости это пережить нетрудно, но в системах, выполняющих автоматическую обработку данных, нужны специальные методы для решения этой проблемы.
Иерархические структуры данных по форме сложнее, чем линейные и табличные, но они не создают проблем с обновлением данных.
Их легко развивать путем создания новых уровней. Даже если в учебном заведении будет создан новый факультет, это никак не отразится на пути доступа к сведениям об учащихся прочих факультетов.
Недостатком иерархических структур является относительная трудоемкость записи адреса элемента данных и сложность упорядочения. Часто методы упорядочения в таких структурах основывают на предварительной индексации, которая заключается в том, что каждому элементу данных присваивается свой уникальный индекс, который можно использовать при поиске, сортировке и т. п. Ранее рассмотренный принцип дихотомии на самом деле является одним из методов индексации данных в иерархических структурах. После такой индексации данные легко разыскиваются по двоичному коду связанного с ними индекса.
Адресные данные. Если данные хранятся не как попало, а в организованной структуре (причем любой), то каждый элемент данных приобретает новое свойство (параметр), который можно назвать адресом. Конечно, работать с упорядоченными данными удобнее, но за это приходится платить их размножением, поскольку адреса элементов данных — это тоже данные, и их тоже надо хранить и обрабатывать.
