Компьютер как инструмент научной работы
Вычислительная мощь компьютера позволяет использовать его как средство автоматизации научной работы. Для решения сложных расчетных задач используют программы, написанные специально. В то же время, в научной работе встречается широкий спектр задач ограниченной сложности, для решения которых можно использовать универсальные средства.
К такого рода задачам относятся, например, следующие:
• подготовка научно-технических документов, содержащих текст и формулы, записанные в привычной для специалистов форме;
• вычисление результатов математических операций, в которых участвуют число вые константы, переменные и размерные физические величины;
• операции с векторами и матрицами;
• решение уравнений и систем уравнений (неравенств);
• статистические расчеты и анализ данных;
• построение двумерных и трехмерных графиков;
• тождественные преобразования выражений (в том числе упрощение), аналитическое решение уравнений и систем;
• дифференцирование и интегрирование, аналитическое и численное;
· решение дифференциальных уравнений;
- проведение серий расчетов с разными значениями начальных условий и других параметров.
К универсальным программам, пригодным для решения таких задач, относится, например, программа MathCad, которая представляет собой автоматизированную систему, позволяющую динамически обрабатывать данные в числовом и аналитическом (формульном) виде. Программа MathCad сочетает в себе возможности проведения расчетов и подготовки форматированных научных и технических документов.
Научно-технические документы обычно содержат формулы, результаты расчетов в виде таблиц данных или графиков, текстовые комментарии или описания, другие иллюстрации. В программе MathCad им соответствуют два вида объектов: формулы и текстовые блоки. Формулы вычисляются с использованием числовых констант, переменных, функций (стандартных и определенных пользователем), а также общепринятых обозначений математических операций.
Введенные в документ MathCad формулы автоматически приводятся к стандартной научно-технической форме записи. Графики, которые автоматически строятся на основе результатов расчетов, также рассматриваются как формулы. Комментарии, описания и иллюстрации размещаются в текстовых блоках, которые игнорируются при проведении расчетов.
Чтобы буквенные обозначения можно было использовать при расчетах по формулам, этим обозначениям должны быть сопоставлены числовые значения. В программе MathCad буквенные обозначения рассматриваются как переменные, и их значения задаются при помощи оператора присваивания (вводится символом «:»). Таким же образом можно задать числовые последовательности, аналитически определенные функции, матрицы и векторы.
Если все значения переменных известны, то для вычисления числового значения выражения (скалярного, векторного или матричного) надо подставить все числовые значения и произвести все заданные действия. В программе MathCad для этого применяют оператор вычисления (вводится символом «=»). В ходе вычисления автоматически используются значения переменных и определения функций, заданные в документе ранее. Удобно задать значения известных параметров, провести вычисления с использованием аналитических формул, результат присвоить некоторой переменной, а затем использовать оператор вычисления для вывода значения этой переменной. Например:
g:=9.8
М:=3
F:=M-g
F=29A
Изменение значения любой переменной, коррекция любой формулы, означает, что все расчеты, зависящие от этой величины, необходимо проделать заново. Такая необходимость возникает при выборе подходящих значений параметров или условий, поиске оптимального варианта, исследовании зависимости результата от начальных условий. Электронный документ, подготовленный в программе MathCad, готов к подобной ситуации. При изменении какой-либо формулы программа автоматически производит необходимые вычисления, обновляя изменившиеся значения и графики. Например, если документ содержит формулы х := 4; vx = 2, то, изменив значение переменной х, мы сразу же увидим, что изменился и результат расчета: х := 9; vх =3.
При проведении расчетов с использованием реальных физических величин учитывают их размерность. Чтобы расчет был корректен, все данные должны быть приведены в одну систему единиц — в этом случае результат расчетов получится в этой же системе. Здесь скрывается характерный источник ошибок при расчетах вручную. В программе MathCad единицы измерения (в любой системе) присоединяют к значению величины с помощью знака умножения. Данные автоматически преобразуются в одну и ту же систему единиц (по умолчанию СИ) и обрабатываются в этом виде. Размерный результат выдается вместе с полученной единицей измерения. Например:
v := 100×kph t:=0.5×yr (kph — километры в час, уr — годы),
s := v×t s = 4.383×108 m (результат получен в метрах).
При работе с матрицами приходится применять такие операции, как сложение матриц, умножение, транспонирование. Часто возникает необходимость в обращении матриц и в декомпозиции (разложении в произведение матриц специального вида). Для квадратных матриц представляет интерес поиск собственных значений и собственных векторов. Программа MathCad позволяет выполнить все эти операции с помощью стандартных обозначений математических операторов (сложение, умножение) или встроенных функций. Например:




Уравнения и системы уравнений, возникающие в практических задачах, обычно можно решить только численно. Методы численного решения реализованы и в программе MathCad. Блок уравнений и неравенств, требующих решения, записывается после ключевого слова given (дано). При записи уравнений используется знак логического равенства (комбинация клавиш CTRL+=). Значения переменных, удовлетворяющие системе уравнений и неравенств, находятся с помощью стандартной функции find.
given
х – у = 2
sin(x)=sin(y)
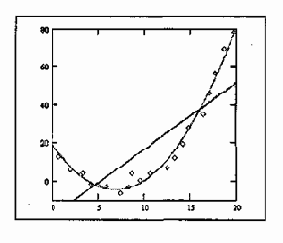 |

Рис. 18.1. Набор точек аппроксимирован с помощью многочленов первого и второго порядка |
Для такого рода задач программа Ма!ИСас1предоставляет средства интерполяции данных, предсказания дальнейшего поведения функции, а также построения функций заданного вида, наилучшим образом соответствующих имеющемуся набору данных. При статистическом анализе можно также использовать стандартные функции распределения вероятности и генераторы случайных величин с заданным распределением.
При аналитических вычислениях результат получают в нечисловой форме в результате тождественных преобразований выражений. Простейшие преобразования — это раскрытие скобок, приведение подобных членов, применение тригонометрических тождеств.
Например, выражение cos (3-atan(x)) преобразуется в

Проверку тождественности этого преобразования выполните самостоятельно.
Более сложные преобразования позволяют находить аналитические решения некоторых уравнений и систем. Для такого рода вычислений в программе MathCad используют оператор аналитического вычисления (клавиатурная комбинация CTRL+.), а также команды меню Symbolics (Аналитические вычисления). Переменные при аналитических вычислениях рассматриваются как неопределенные параметры. Результат можно использовать для анализа решения при различных значениях этих переменных. При аналитическом решении уравнений и систем за одну операцию можно найти все существующие решения. Например:
given

find(z)

Дифференцирование и интегрирование заданных функций вручную — обычно несложная, но трудоемкая операция. В программе MathCad для вычисления производной, а также неопределенных и определенных интегралов могут использоваться символические вычисления с помощью меню Symbolics > Variable (Аналитические вычисления > Переменная). Если функция не задана аналитически или не позволяет получить первообразную в виде формулы, имеется возможность численного дифференцирования и численного расчета определенных интегралов. Например, при вычислении интеграла

получается правильный результат:

Численные методы используют и для решения дифференциальных уравнений. С помощью программы MathCad можно решать уравнения и системы уравнений первого порядка с заданными начальными условиями. Уравнение более высокого порядка надо сначала преобразовать в систему уравнений первого порядка.
